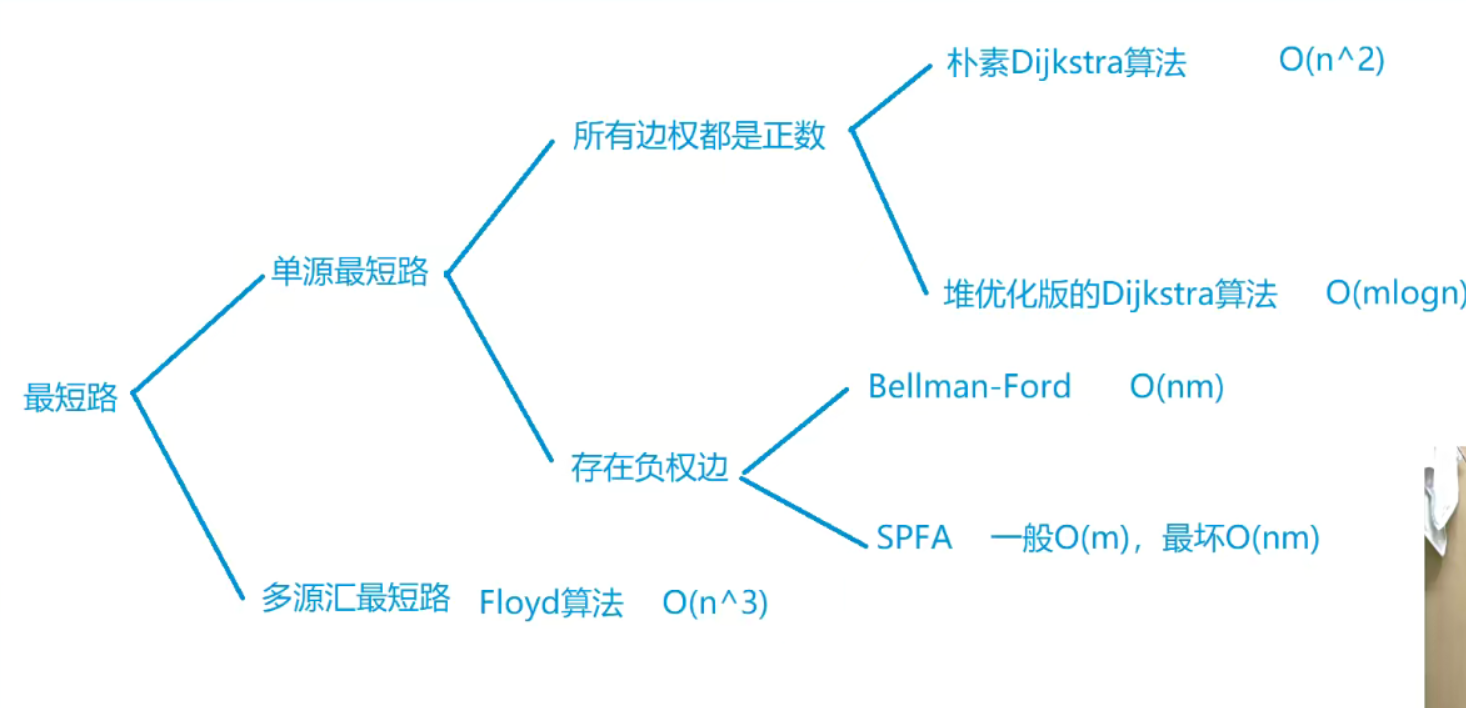
图的单源最短路径

1.无权图的最短路径

本质：利用bfs，第一次到达顶点时即为最短路径

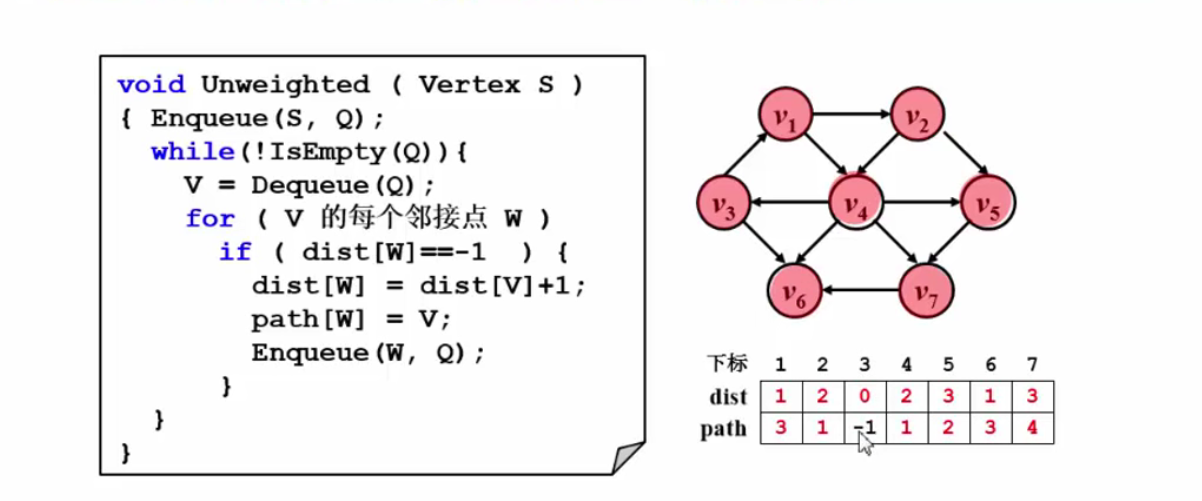
image.png

2.有权图的最短路径

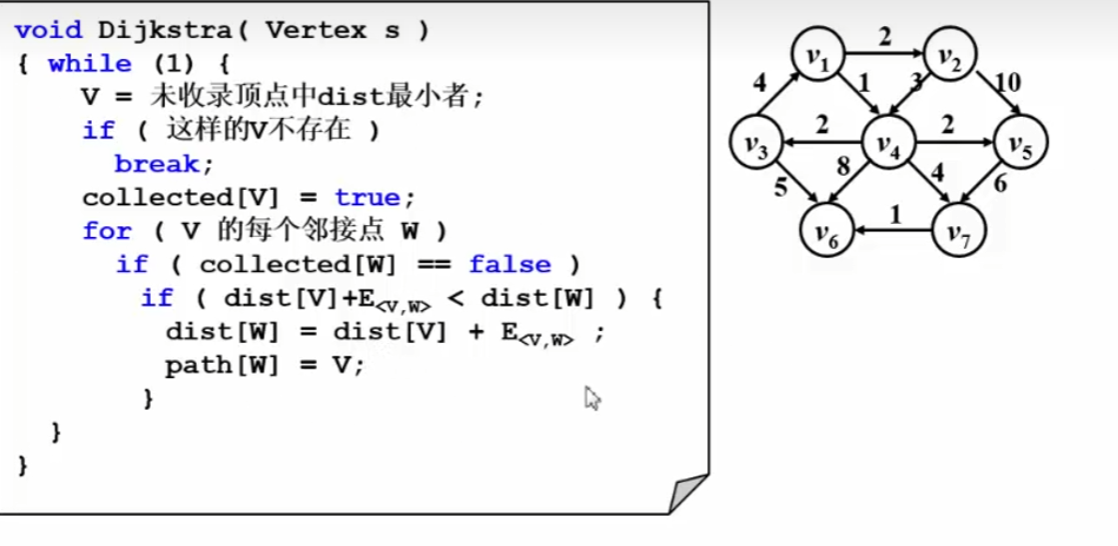
image.png
collected[v] 表示v顶点已经计算完成
之后判断V的每个邻接点 W ： 从V点走到W距离是否小于当前距离，如果是就更新
注意每次的V是当前dist最小距离！

dist[S] = 0
for(int i = 1;i<=n;i++)
{
  int t = -1;
  for(int j = 1;j<=n;j++)
  {
     if(!vis[j] && (t == -1 || dist[t] > dist[j]))
     {
        t = j;
     }
  }
  vis[t] = true;
  for(int j = 1;j<=n;j++)
  {
     if(w[t][j] != 0 && !vis[j])
     {
	      dist[j] = max(dist[j],dist[t]+w[t][j];
	      path[j] = t;
     }
  }
}

3. Bellman——Ford

Bellman-Ford算法大致可以分成三部分：

  1. 初始化所有d[s],源点d[s]=0,其他d[s]=INF

  2. 进行 n-1次循环，在循环体中遍历所有的边，进行松弛计算（if(d[v]>d[u]+w[u][v]) d[v]=d[u]+w[u][v]

  3. 遍历图中所有的边，检验是否出现这种情况：d[v]>d[u]+w[u][v] ,若出现则返回 false,没有最短路

正常循环完成后所有最短路径都找到，但仍然出现可松弛计算，说明有负值路径

在算法题中并不会真正保存所有边，在初始化的时候保证不相连的两条边值为无穷大这样直接循环所有顶点即可

for (int k = 1; k <= n; k++)
    {
        for (int i = 1; i <= n; i++)
            {
                for (int j = 1; j <= n; j++)
                    {
                        d[i][j] = min(d[i][j],d[i][k]+d[k][j]);
                    }
            }
    }

d[i][j]表示的是 i —— j 的最短距离 ， 刚开始输入 d[i][j] 表示两点间边的距离

总结

n表示点数，m表示边的个数
image.png